Test case - \mathrm{LiFeSO_4F}

Test case - \(\mathrm{LiFeSO_4F}\)#

Here, we use M3GNet to search for low energy \(\ce{LiFeSO4F}\) structures. The DFT results have been previously published here: https://aip.scitation.org/doi/full/10.1063/5.0076220.

The search for \(\ce{LiFeSO4F}\) is more challenging, because the Materials Project database does not have extensive data on the low energy polymorphs. In the work above, we have found several new polymorphs which are not present in the Materials Project database.

Hide code cell source

 
import os
os.environ["CUDA_VISIBLE_DEVICES"]="-1"    

import warnings
from pathlib import Path
from ase.io import read
import ase
# from m3gnet.models import Relaxer
# from pymatgen.ext.matproj import MPRester
from pymatgen.core import Structure

import pandas as pd

from tqdm import tqdm
tqdm = lambda x: x

## Loading data
lifeso4f_mp = Structure.from_file("LiFeSO4F-mp-943492.vasp")

lifeso4f_mp_relaxed = read("exp-m3gnet/LiFeSO4F-mp-943492.res")
lifeso4f_mp_relaxed_energy = lifeso4f_mp_relaxed.info['energy']  / len(lifeso4f_mp_relaxed)
lifeso4f_mp_relaxed_volume = lifeso4f_mp_relaxed.get_volume() / len(lifeso4f_mp_relaxed)

Hide code cell source

 
def load_dataset(names):
    cells = [read(x) for x in  tqdm(names)]
    for atoms, name in zip(cells, input_names):
        atoms.info['fname'] = name.stem

    dataset = []
    for atoms in cells:
        dataset.append(
        {
            'atoms': atoms,
            'label': atoms.info['fname'],
            'energy': atoms.info['energy'],
            'energy_per_atom': atoms.info['energy'] / len(atoms),
            'volume': atoms.get_volume(),
            'volume_per_atom': atoms.get_volume() / len(atoms),

        }
        )

    return pd.DataFrame(dataset).sort_values('energy_per_atom')

def show_compact(df):
    return df[['label', 'energy_per_atom', 'volume_per_atom']]

Hide code cell source

 
input_names = list(Path("LiFeSO4F-run1").glob("*.res"))
df_dft = load_dataset(input_names)

input_names = list(Path("LiFeSO4F-run1-m3gnet").glob("*.res"))
df_m3g = load_dataset(input_names)

input_names = list(Path("LiFeSO4F-relaxed-m3gnet").glob("*.res"))
df_relaxed_m3g = load_dataset(input_names)

Energy - Volume distribution#

Similar to the \(\ce{LiFePO4}\), we plot the energy per atom against the volume per atom.

Hide code cell source

 
def add_labels(ax):
    """Add axis labels"""
    ax.set_ylabel('Energy per atom (eV)')
    ax.set_xlabel(r'Volume per atom ($\mathrm{\AA^3}$)')

ax = df_m3g.plot.scatter('volume_per_atom', 'energy_per_atom', label='m3gnet', s=4)
ax = df_relaxed_m3g.plot.scatter('volume_per_atom', 'energy_per_atom', label='DFT relaxed -> m3gnet', ax=ax, color='C1', s=3)
ax.scatter( [lifeso4f_mp_relaxed_volume], [lifeso4f_mp_relaxed_energy],  marker='d', color='r', label='Experimental')
min_eng = df_m3g.energy_per_atom.min()
#ax.set_xlim(10, 15)
ax.set_ylim(min_eng-0.01, min_eng+ 0.05)
ax.legend(loc=1)
add_labels(ax)
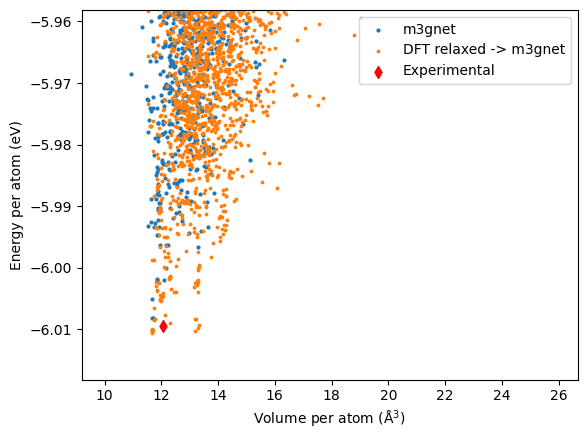
_images/7f0c06c0e904eaec4d9f492e2df9f6ab00f9eff06c6a81a9762937ec51abe9a4.png

Hide code cell source

 
ax = df_dft.plot.scatter('volume_per_atom', 'energy_per_atom', 
                         #xlim=(9, 14), ylim=(-434, -433.75), 
                         label='PBE + U Search')
min_eng = df_dft.energy_per_atom.min()
ax.set_ylim(min_eng-0.01, min_eng+ 0.05)

ax.legend(loc=1)
add_labels(ax)
_images/62fe65657c9bc94ea4c9bbdc412b53d45ae4f1c2de4a6fee4daf1a7a2ecf6f93.png

Top structure found in each case are shown below. In this case, the M3GNet gives completely different low energy structures which are different to the experimentally found tavorite structure. This is also shown in the distribution plot above where the orange dots do not overlap with the red diamonds (experimental structure).

Hide code cell source

 
show_compact(df_m3g.iloc[:5])
label energy_per_atom volume_per_atom
622 2LiFeSO4F-200804-055229-a4aef3 -6.008125 11.683317
2286 2LiFeSO4F-200804-043547-80a807 -6.008113 11.704279
2002 2LiFeSO4F-200818-200625-fa2e89 -6.005019 11.657444
474 2LiFeSO4F-200804-031846-78332d -6.001975 12.084385
2784 2LiFeSO4F-200819-000200-50146f -6.001975 11.862633

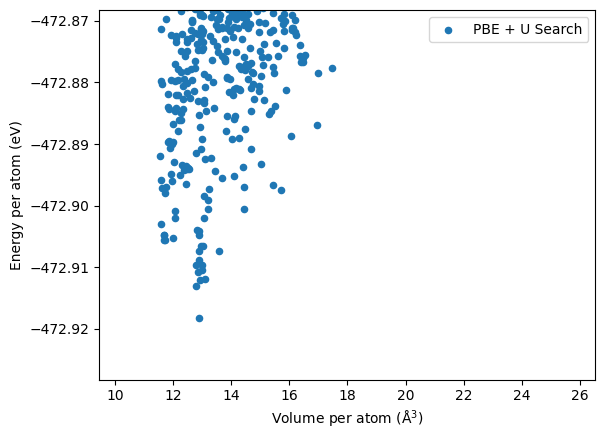
On the other hand, re-relaxing the DFT relaxed structure gives different sets low energy structures, one has a volume per atom of about 11.8 \(\mathrm{\AA^3}\) while the other has a volume of about 13.2 \(\mathrm{\AA^3}\).

Hide code cell source

 
show_compact(df_relaxed_m3g.iloc[:5])
label energy_per_atom volume_per_atom
246 2LiFeSO4F-200818-173807-f55f90 -6.010575 11.660858
2488 4LiFeSO4F-200804-093629-270f26 -6.010425 11.663456
2286 2LiFeSO4F-200804-043547-80a807 -6.010275 11.670359
301 2LiFeSO4F-200804-034722-678938 -6.010187 13.186974
2784 2LiFeSO4F-200819-000200-50146f -6.010144 11.676132

In fact, the sets of low energy structures with large volumes contains the new polymorphs found in the DFT search previously. Structure f55f90 (in df_relaxed_m3g) and a4aef3 in (df_m3g) has almost the same structure but the energies are different by 2 meV and almost identical structures have been found for them separately.

Hide code cell source

 
show_compact(df_dft.iloc[:3])
label energy_per_atom volume_per_atom
301 2LiFeSO4F-200804-034722-678938 -472.918226 12.890395
2434 2LiFeSO4F-200804-022644-43b3f4 -472.913076 12.803132
3860 2LiFeSO4F-200804-022154-9da9fb -472.912053 12.918566

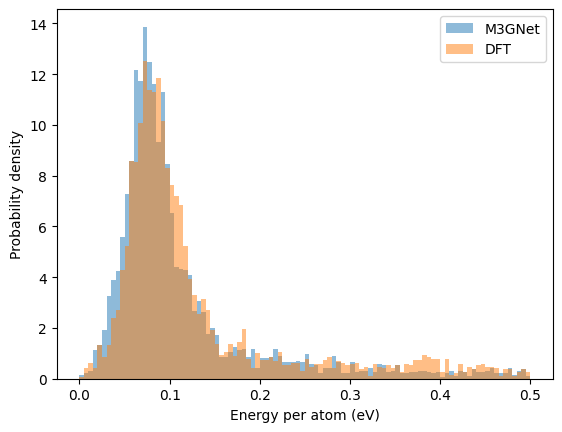
Energy distribution of the relaxed structures#

M3GNet seems to give an energy distribution among the relaxed structure very similar to that of the DFT.

Hide code cell source

 
import matplotlib.pyplot as plt

engs = df_m3g['energy_per_atom'].values.copy()
engs_m3g = engs - lifeso4f_mp_relaxed_energy
engs = df_dft['energy_per_atom'].values.copy()
engs_dft = engs - engs.min()

plt.hist(engs_m3g, bins=100,alpha=0.5, density=True, range=(0, 0.5), label='M3GNet');
plt.hist(engs_dft, bins=100, alpha=0.5, density=True, range=(0, 0.5), label='DFT');
plt.legend()
plt.xlabel('Energy per atom (eV)')
plt.ylabel('Probability density');
_images/a254790a0623e0b31fa6546e750eec64b977e922cd1e690c43794ca1b7724e69.png

Discussion#

Search using M3GNet for relaxation is not able to fully reproduce the DFT results, and it tends to find a cluster of structure with smaller volumes. On the other hand, M3GNet does give a reasonable good description for the low energy structures. In particular, the DFT lowest energy structure 678938 is also found to be one of the lowest energy structure when the DFT relaxed structure is further relaxed using M£GNet. This suggests that M3GNet does well when interpolating - even if there are little \(\ce{LiFeSO4F}\) data in the training set, there are plenty of training data in the composition space of Li-Fe-S-O-F.

Contents